Evaluating the number of hidden layers in a neural network

As the number of practitioners in the field of data science is ever-increasing, there is a growing demand for understanding the learning characteristics of artificial neural networks (ANNs). The Cambrian explosion in deep learning has resulted in the exponential growth of information surrounding ANNs, and how they are designed, implemented, trained, tested, and evaluated.   In this article, we address the relationship between class prediction accuracy for classification problems (datasets) as a function of the number of hidden layers employed.

Class prediction accuracy was determined as a function of the number of hidden layers of a feed-forward back-propagation ANN for 12 public datasets obtained from the UCI Machine Learning repository.   A modified version of NXG Logic Explorer was used for the ANN hidden layer evaluation. Feature selection was not performed for the input datasets, rather, all input features were used. ANN construction involved mean-zero standardizing each input feature's value, and clamping each input object to the input nodes.   Upon initialization, all connection weights were set to random values in the range [-0.5,0.5]. The activation function at each node in the hidden layers was the logistic function.   The MSE was set to 1/2*sum(y_c - t_c)^2.

A total of 300 sweeps through the data were used.   In the first run, object order was permuted at the beginning of each sweep to prevent the ANN from learning anything related to object order. In the second run, bootstrapping was performed at the beginning of each sweep to construct a dataset whose sample size was equal to the original dataset, but could have duplicate objects due to sampling with replacement.

Recall, the intent was not to perform 2-, 5-, or 10-fold CV, LOOCV, or bootstrap bias by training with objects not in the test folds, but rather to get a handle on how the predictive accuracy breaks down as a function of the number of hidden layers employed.   For each hidden layer, the number of nodes used was based on the geometric pyramid rule.

Results indicate that, when permuting objects during each sweep, for most of the datasets the recall accuracy dropped when more than two hidden layers was employed.   This is due to the increasing instability of the gradient as hidden layers are added. ("Overfitting" and "underfitting" are terms typically related to having too many or too few nodes in a hidden layer, respectively). Several of the datasets showed no improvement in accuracy beyond use of one hidden layer, which is in agreement with the general rule of thumb that using more than one hidden layer does not result in improved performance.   However, since several of the datasets showed greater accuracy when two hidden layers were used, our recommendation is to use two hidden layers.   The average recall accuracy was greatest for two hidden layers, so this finding supports our recommendation for using 2 hidden layers.

For the second run, during sweeps the data were bootstrapped to construct a new dataset with the same sample size by sampling objects with replacement. On average, when randomly sampling objects with replacement during bootstrap construction of a dataset (i.e., each object is placed back into the pool of objects after random selection and can be sampled again), the probability that each object is not selected is 0.368, while the probability that each object is selected is 0.632. Bootstrapping is a commonly used technique in computer science for overcoming the challenge associated with not knowing if a dataset is reliable.

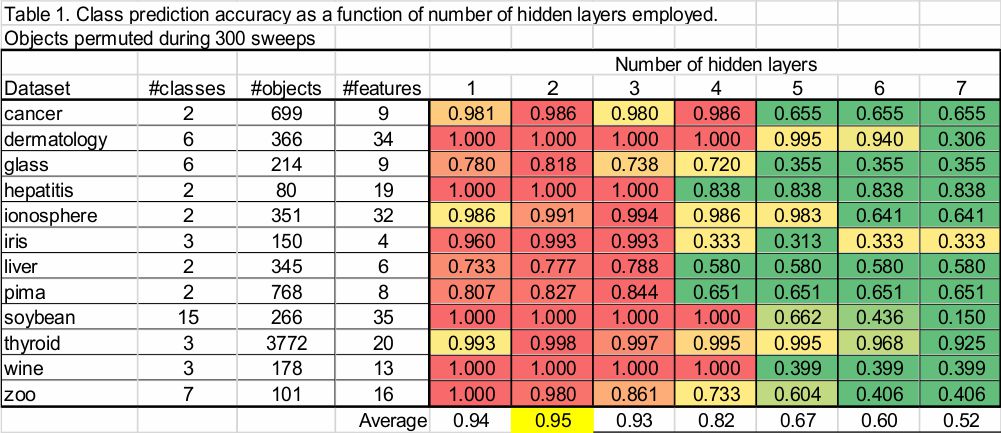
The ANN classification accuracy when bootstrapping during sweeps was similar to the results obtained when permuting objects during sweeps, in that class predictive accuracy dropped after more than 2 hidden layers were employed. Bootstrapping results also did not overestimate permutation results, suggesting the more conservativeness from bootstrapping.

In conclusion, the following rules of thumb are inferred from the empirical data:

If more than one hidden layer is not technically available (based on the software being used), then one hidden layer should be used.
However, if two hidden layers can be employed, then use this as a default, since our results indicate the greatest average recall accuracy when two hidden layers were employed (permuted objects results).
Beyond two hidden layers, there will likely be a drop in performance of an ANN.

There are occassions when using more than two hidden layers is beneficial. This occurs when complex objects are encountered such as during hand-written character recognition or facial recognition. Non-linear function approximation with multiple input dimensions (features) will also generally result in a better fit (lower RMSE) when using 2 or more hidden layers. In fact, recovery of a 3D surface curve when only one hidden layer is used will commonly degrade the peaks of Gaussian hilltops and valleys, and introduce ridges in the flat section where Z=0. Whereas, when a second hidden layer is employed, the maxima and minima of Gaussian peaks and valleys will be recovered, and the flat areas of the landscape will be more smoothly approximated at Z=0.